Funkce (matematika) – Wikipedie
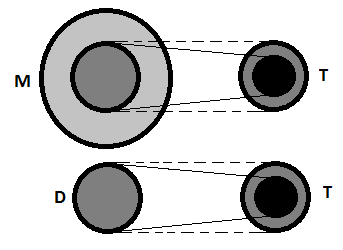
Funkce je v matematice název pro zobrazení z množiny M na nebo do číselného tělesa T (množiny reálných nebo komplexních čísel), či na nebo do vektorového prostoru T m } tvořeného uspořádanými m -ticemi
Funkce › Matematika › Uč se online! - Vše co potřebuješ do…
Funkce Funkce je naprosto zásadní pojem v matematice, kterému byste měli plně rozumět. Matematika je protkaná funkcemi a kdejaký symbol, který znáte od základní školy, ve skutečnosti představuje funkci.
Matematické funkce | Edufix.cz
Uvedeme zjednodušenou definici funkce jedné proměnné a na příkladech si ji objasníme. Funkce je předpis, který každému x přiřazuje právě jedno y.
Funkce – Sociologická encyklopedie
Funkce – (z lat. functio = vykonávání, úkon, činnost) – v tradičním matem. významu závislost mezi dvěma proměnnými, předpis, podle něhož se prvkům x množiny M, které se nazývají argumenty f., přiřazují určité prvky y z množiny M.
Funkce – Umíme to
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
- Funkce
- Základní typy funkcí
- Vlastnosti funkcí
- Grafy funkcí
- Grafy lineárních funkcí
- Grafy kvadratických funkcí
- Grafy mocninných funkcí
- Grafy goniometrických funkcí
- Grafy logaritmických funkcí
- Grafy lineárních nerovnic
- Souřadnice bodů v rovině
- Lineární funkce
- Vlastnosti lineární funkce
- Lineární lomené funkce
- Kvadratické funkce
- Vlastnosti kvadratické funkce
- Kvadratické rovnice
- Goniometrické funkce
- Mocninné funkce
- Exponenciální funkce
- Logaritmické funkce
Funkce – Příklady z matematiky
Zobrazíme-li větší počet bodů a spojíme je souvislou čarou, vznikne graf funkce.
Matematické funkce - úplné základy
Tento článek jsem se rozhodl vytvořit, abych byl schopen všem vysvětlit, jak matematika ve fyzice funguje. K fyzice matematika jednoznačně patří, a proto chci, aby ji čtenář při sledování mého kurzu uměl.
Funkce | Slovník cizích slov
Co znamená podstatné jméno funkce? Význam slova funkce ve slovníku cizích slov včetně překladů do angličtiny, nemčiny, francouzštiny, italštiny, španělštiny, ruštiny, latiny a polštiny.
Funkce
Máme-li funkci, která není ani rostoucí, ani klesající na svém definičním oboru, můžeme tento definiční obor omezit a tato nová funkce už může být klesající.
Funkce je v matematice název pro zobrazení z množiny M na nebo do číselného tělesa T (množiny reálných nebo komplexních čísel), či na nebo do vektorového prostoru T m tvořeného uspořádanými m -ticemi prvků z číselného tělesa T v případě vektorové funkce. Je to tedy předpis, který každému prvku z množiny D ⊆ M (kde Wikipedie
odkazuje na služby nejen od Seznam.cz.
© 1996–2025 Seznam.cz, a.s.