Heavisideova funkce – Wikipedie
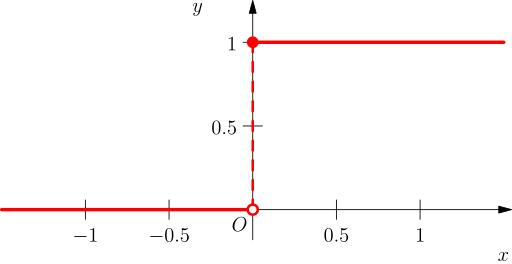
Heavisideova funkce (také jednotkový skok) je nespojitá funkce, jejíž hodnota je nulová pro zápornou hodnotu argumentu a rovna jedné pro kladnou hodnotu argumentu.
Diskuse:Heavisideova funkce – Wikipedie
Pokud by se tam funkce nedefinovala, tak by to nefungovalo vůbec.
Math Tutor - Functions - Theory - Elementary Functions
Heavisideova funkce je definována pro reálná čísla vztahem
Zneuznaný génius Oliver Heaviside | Matfyz.cz
Málokdo ví, že slavné Maxwellovy rovnice, které daly základ teorii elektromagnetického pole, nejsou tak úplně dílem skotského fyzika Jamese Maxwella. Původních 20 Maxwellových rovnic totiž na známé čtyři zredukoval anglický učenec Oliver…
Náběhová funkce – Wikipedie
Náběhová funkce (neboli též funkce rampy) je označení pro základní reálnou funkci definovanou takto:
Detail předmětu – VUT
Elementární funkce komplexní proměnné. 3. Derivace funkce komplexní proměnné, holomorfní funkce, Cauchy-Riemannovy rovnice. 4. Harmonická funkce.
a následně −∇ ×
Zachování náboje proto vyžaduje J = −vσ 0 ať už je Θ přímo Heavisideova funkce, nebo nějaká jiná funkce s méně extravagantní derivací.
Integrální a diskrétní transformace
Laplaceova transformace - základní vlastnosti, aplikace na řešení úloh pro obyčejné a parciální diferenciální rovnice. Diskrétní Laplaceova transformace a Z-transformace - základní vlastnosti, aplikace při řešení diferenčních rovnic.
Heavisideova funkce (také jednotkový skok) je nespojitá funkce, jejíž hodnota je nulová pro zápornou hodnotu argumentu a rovna jedné pro kladnou hodnotu argumentu. Hodnota funkce pro nulový argument není podstatná a proto je různými autory definována odlišně (viz níže). Často se používá v teorii řízení a při zpracování signálu, kde slouží k reprezentaci jednorázové změny signálu. Pojmenována byla po anglickém učenci Oliveru Heavisideovi. Wikipedie
odkazuje na služby nejen od Seznam.cz.
© 1996–2025 Seznam.cz, a.s.