Mocninná funkce – Wikipedie
Mocninná funkce je elementární matematická funkce, jejíž hodnoty jsou přímo úměrné určité mocnině proměnné.
Mocninné funkce | Funkce | Metodika výuky středoškolské…
Mocninné funkce probírané na střední škole se zaměřují na funkce typu $f:y=x^n$ a $g:y=x^ $, kde $n \in N$. Pro čtyři typy exponentů (kladný sudý, kladný lichý, záporný sudý a záporný lichý) musí studenti bez zaváhání načrtnout jeden ze čtyř…
Mocninná funkce s přirozeným exponentem
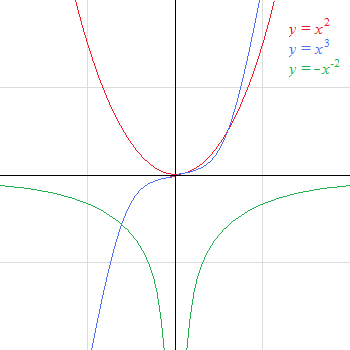
Vlastnosti mocninné funkce se suchým a lichým exponentem, grafy sudé a liché funkce, inverzní funkce
Funkce
Ze základní školy víme, že pro všechna \(x\in\mathbb R\) a pro všechna \(n\in\mathbb N\) (kde množina \(\mathbb N=\ \ platí vztah
Mocninné funkce - Matematika - Maturitní otázky
Mocninná funkce je funkce dána vztahem , kde . Základní grafy: sudé sudá pro klesající pro rostoucí není prostá omezená zdola minimum v bodě nemá maximum liché lichá rostoucí prostá neomezená ani maximum, ani minimum sudé sudá pro rostoucí…
Mocninná funkce je elementární matematická funkce, jejíž hodnoty jsou přímo úměrné určité mocnině proměnné. Mocninná funkce s reálným exponentem r je funkce ve tvaru: f : x ↦ a x r = a e r ln x a , r ∈ R , =ae^\qquad a,r\in ,} kde a ≠ 0 a r ≠ 0 Wikipedie
odkazuje na služby nejen od Seznam.cz.
© 1996–2025 Seznam.cz, a.s.